
RIES
Research Institute for Electronic Science, Hokkaido University
北海道大学
電子科学研究所

LAST UPDATE 2017/02/25
-
研究者氏名
Researcher Name長山雅晴 Masaharu NAGAYAMA
教授 Professor -
所属
Affiliation北海道大学 電子科学研究所
人間数理研究分野
Research Institute for Electronic Science, Hokkaido University
Mathematical Modeling Lab. -
研究キーワード
Research Keywords数理モデリング
反応拡散系
数値シミュレーション
数値分岐解析
Mathematical modeling
Reaction-diffusion systems
Numerical simulations
Numerical bifurcation analysis
- 研究テーマ
Research Subject -
非線形現象に対する数理モデリングとその数理解析
Mathematical modeling and analysis of nonlinear phenomena
研究の背景 Background of the Research
具体的な現象に対する数理モデリング,数値シミュレーション,数学解析を積み重ねることによって,数学・数理科学的研究は現象に対して普遍的数理構造を抽出することができ,複数の異なる現象の本質的なメカニズムに共通の理解を与えることができます.そのためには,現象に対する数理モデリングが重要であり,その方法論を確立することは大きな課題となっています.
Through a combination of mathematical modeling, numerical simulation and analysis of concrete phenomena, the mathematical sciences provide a framework for extracting underlying structures which can be used in understanding the common and essential mechanisms of various phenomena. Here, mathematical modeling of the phenomena is of great importance and a main hurdle lies in establishing appropriate methodologies for its analysis.
研究の目標 Research Objective
様々な非線形現象に対して数理モデリング化を行い,数値シミュレーション・数学解析を行うことで,現象の起こるメカニズムを理論的に明らかにすることを目標としています.具体的な研究対象は,自走粒子や液滴の運動,細胞分裂・細胞運動,発生過程にみられる分化波,マウスの脳の発生過程でみられる細胞核運動,表皮バリア機能の恒常性機能の形成,燃焼合成反応等です.また,数理モデリングの解析に必要な数値計算法の開発も目標としています.
The main objective of our research is to provide theoretical clarification of mechanisms giving rise to different nonlinear phenomena. Here we utilize methods of mathematical modeling, simulation and analysis. Concrete examples include: the self-driven motion of particles and liquid droplets, division and motion of biological cells, waves observed in developmental processes, nuclear motions observed in mouse brain development, formulation of homeostasis in the epidermal barrier function, and combustion synthesis reactions. We also develop numerical methods for analyzing mathematical models.
研究図Figures
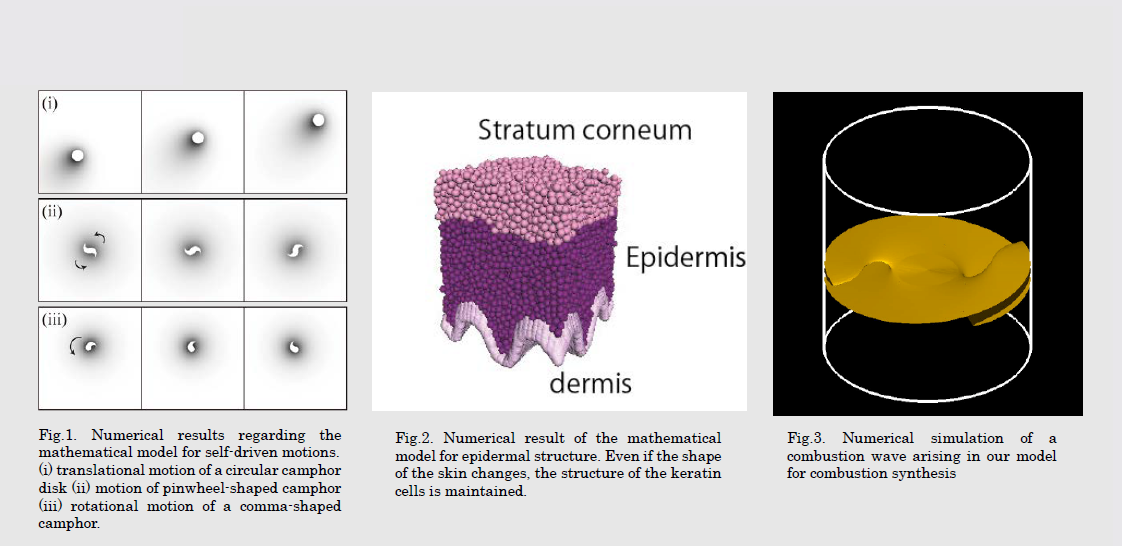
論文発表 / Publications
Physica D, 272, 39-50 (2014), PLoS ONE 9(3): e92650 (2014), J. Materials Synthesis and Processing 9(3), 153-163 (2001)
研究者連絡先 / HP
- nagayama
 es.hokudai.ac.jp
es.hokudai.ac.jp - http://www-mmc.es.hokudai.ac.jp/index.html