
RIES
Research Institute for Electronic Science, Hokkaido University
北海道大学
電子科学研究所

LAST UPDATE 2024/08/09
-
研究者氏名
Researcher Name石井宙志 Hiroshi ISHII
助教 Assistant Professor -
所属
Affiliation北海道大学 電子科学研究所
人間数理研究分野
Research Institute for Electronic Science, Hokkaido University
Mathematical Modeling Lab. -
研究キーワード
Research Keywords反応拡散系
非局所効果
パターン形成
非線形解析
Reaction diffusion systems
Nonlocal effects
Pattern formation
Nonlinear analysis
- 研究テーマ
Research Subject -
反応拡散系におけるパターン形成問題
Pattern formation problems in reaction-diffusion systems
研究の背景 Background of the Research
反応拡散系は物質間の反応と物質の拡散の効果によって,物質の量(濃度や密度など)の空間分布が時間発展する過程を記述する偏微分方程式で,生物学や化学などをはじめとする様々な分野の数理モデルで現れます.そのような数理モデルを用いて現象における普遍的な数理構造を捉えるためには,数学解析・モデリングの方法論を拡充していく必要があります.また,その方法論を応用することで,現象の理解を深めていくことに繋がります.
Reaction-diffusion systems are partial differential equations that describe the time evolution of the spatial distribution of quantities of substances (concentration, density, etc.) because of reactions between substances and the diffusion of substances. The systems appear in mathematical models in various fields such as biology and chemistry. It is necessary to expand the methodologies of mathematical analysis and modelling to capture the universal mathematical structure of phenomena using such mathematical models. The application of such methodologies also leads to a deeper understanding of the phenomena.
研究の目標 Research Objective
反応拡散系や関連する非局所効果を持つ数理モデルに現れる,空間パターンの時間変化をシンプルに表現する方法論の構築を目指しています.例えば,多成分の時間発展を記述する数理モデルを縮約して1・2成分の時間発展を記述する数理モデルを導出する方法論を研究しています.これにより数学解析で扱いやすくなり,数値計算だけでは見えてこない数理モデルのより深い数理構造が捉えることに役立ちます.
The aim of the project is to develop methodologies for the simple representation of temporal changes in spatial patterns that appear in reaction-diffusion systems and related mathematical models with non-local effects. For example, we are working on methodologies to derive mathematical models that describe the time evolution of one or two components by reducing mathematical models that describe the time evolution of multi-components. This makes them easier to handle in mathematical analysis and helps to capture the deeper mathematical structure of mathematical models that cannot be seen by numerical calculations only.
研究図Figures
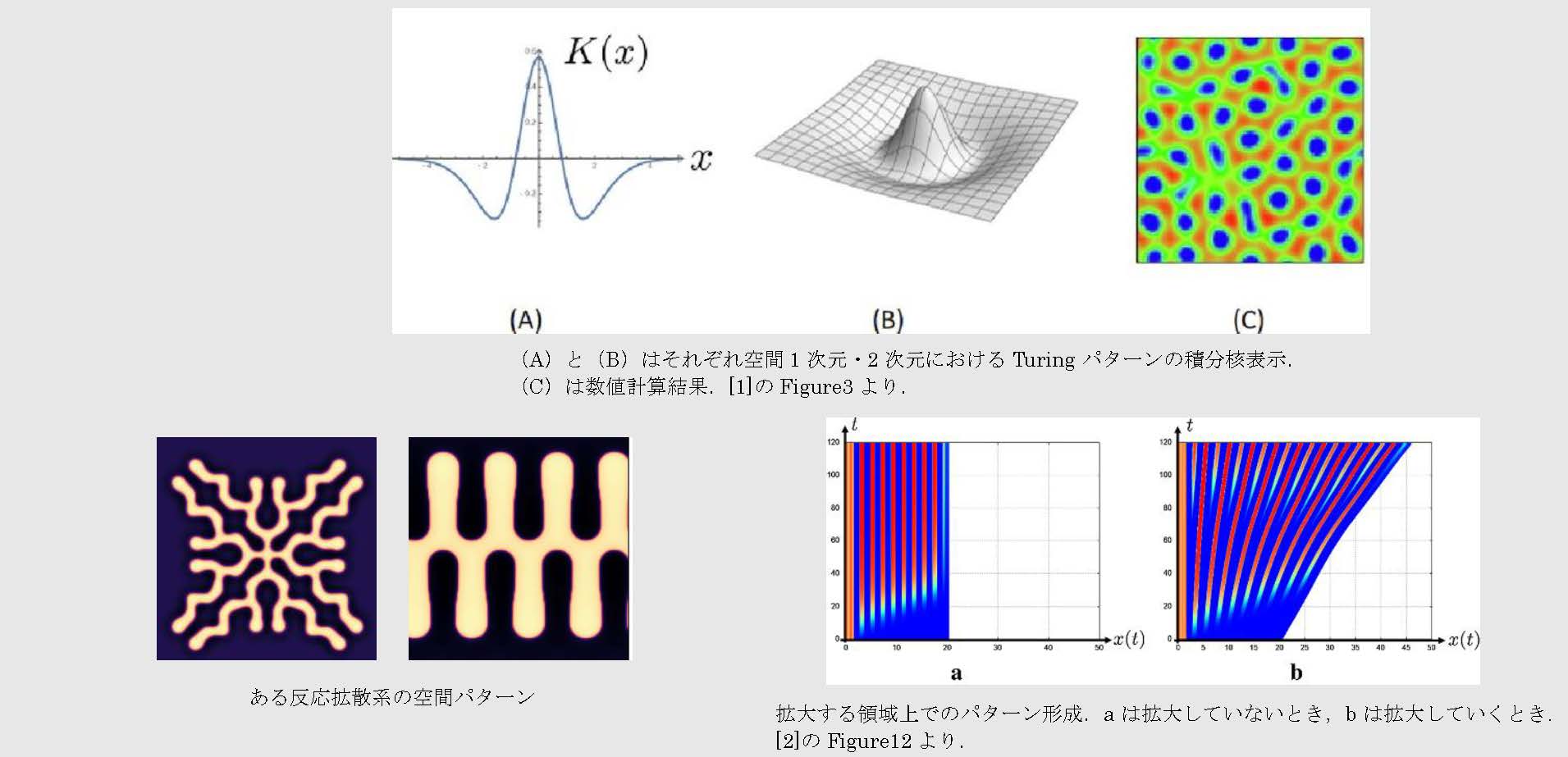
(C)は数値計算結果.[1]のFigure3より.
ある反応拡散系の空間パターン
拡大する領域上でのパターン形成.aは拡大していないとき,bは拡大していくとき.
[2]のFigure12より.
論文発表 / Publications
[1] S.-I. Ei, H. Ishii, S. Kondo, T. Miura, Y. Tanaka, Journal of Theoretical Biology, 509, (2021), 110496, 17pages.
[2] S.-I. Ei, H. Ishii, M. Sato, Y. Tanaka, M. Wang, T. Yasugi, Journal of Mathematical Biology, 81, 981-1028 (2020).
研究者連絡先 / HP
- hiroshi.ishii
 es.hokudai.ac.jp
es.hokudai.ac.jp - https://sites.google.com/view/ishii-hiroshi/.